此文將會一一審視各種資料尺度允許的數學操作以及視覺化方式。每個資料尺度範例以單個欄位做示範,但不限於此單欄位,可應用在其他同樣資料尺度的欄位。
titanic各欄位的資料尺度:
| 欄位 | 資料尺度 |
|---|---|
| PassengerId | 名目尺度 |
| Survived | 名目尺度 |
| Pclass | 次序尺度 |
| Name | 名目尺度 |
| Sex | 名目尺度 |
| Age | 等比尺度 |
| SibSp | 等比尺度 |
| Parch | 等比尺度 |
| Fare | 等比尺度 |
| Cabin | 名目尺度 |
| Embarked | 名目尺度 |
符合此資料尺度的欄位為:PassengerId/Survived/Cabin/Embarked。在名目尺度下,我們不能使用任何定量的數學操作,例如四則運算或乘除。但是我們能使用基本的計數,也就是計算每個值的數量。
#匯入maplotlib做視覺化
import matplotlib.pyplot as plt
#讀取資料
data = pd.read_csv('data/train.csv')
#對所有值計數
data.Embarked.value_counts()
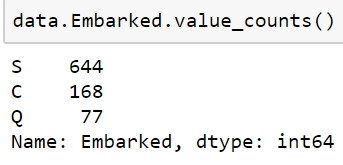
Embarked是乘客上船的港口,S是Embarked最常出現的類別,代表最多人上船的港口。由於可以計數,因此我們可以使用一些挑型圖來做視覺化,例如長條圖與圓餅圖。
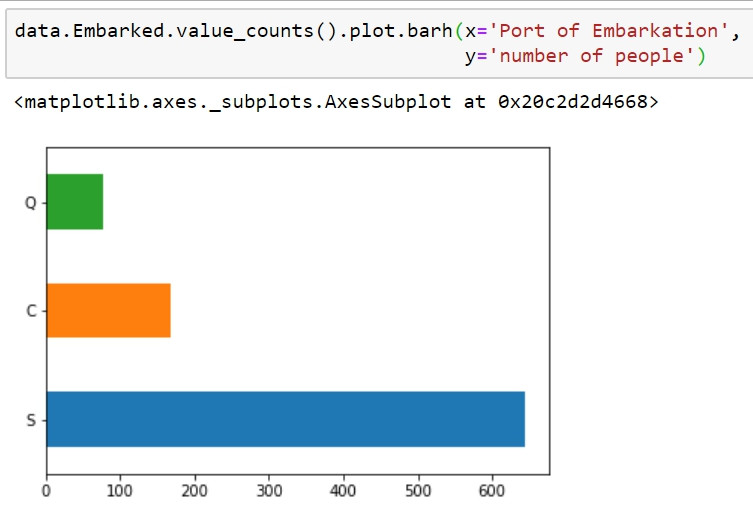
data.Embarked.value_counts().plot.barh(x='Port of Embarkation',
y='number of people')
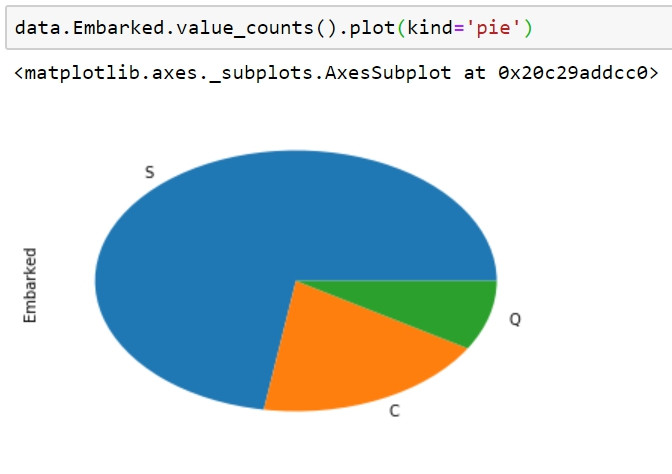
data.Embarked.value_counts().plot(kind='pie')
無
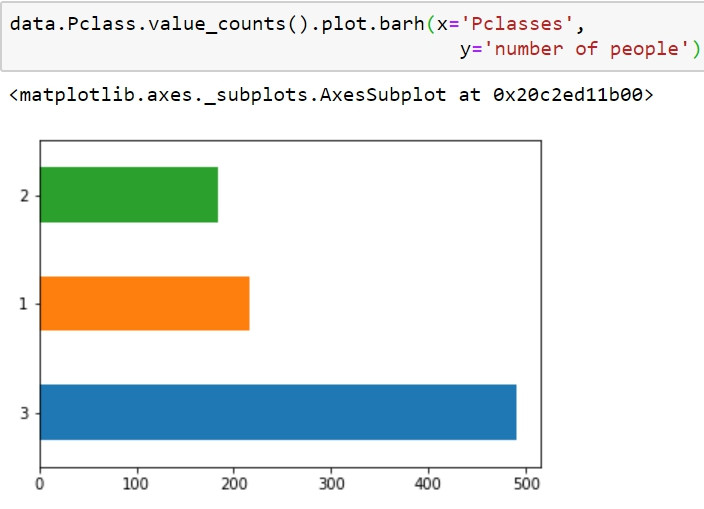
符合此資料尺度的欄位為:Pclass。與名目尺度相比,我們在次序尺度上有一些新的能力。在次序尺度上,我們仍然可以像在名目尺度上那樣進行基本計數,但我們也可以在比較中引入比較和排序。因此,我們可以在此級別使用新圖表。我們可以使用像名目尺度那樣的長條和圓餅圖,但因為我們現在有了排序和比較,我們可以計算中位數和百分位數。有了中位數和百分位數,便能以箱形圖作呈現。
#對所有值計數
data.Pclass.value_counts()
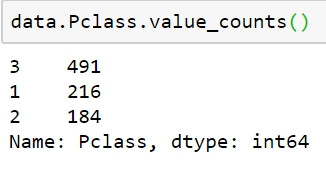
data.Pclass.value_counts().plot.barh(x='Pclasses',
y='number of people')
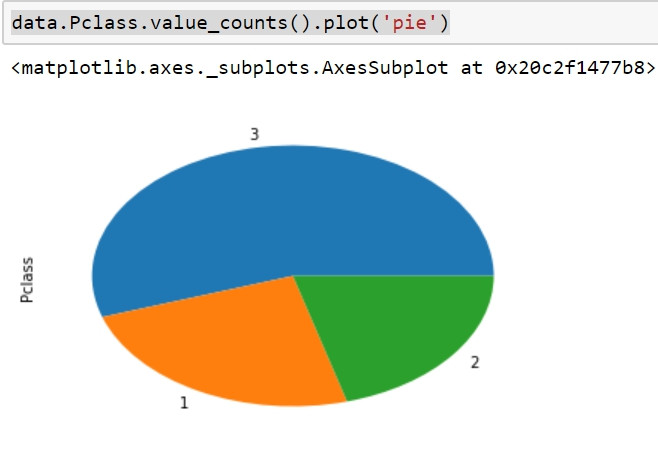
data.Pclass.value_counts().plot('pie')
data.Pclass.value_counts().plot('box')

由於次序尺度相較名目尺度多了排序及大小比較,因此我們能夠使用數值比較的操作。
#只取Pclass為1的紀錄
class_1 = data.Pclass[data.Pclass == 1]
#只取Pclass為2的紀錄
class_2 = data.Pclass[data.Pclass == 2]
#只取Pclass為3的紀錄
class_3 = data.Pclass[data.Pclass == 3]
#只取Pclass大於1的紀錄
below_1 = data.Pclass[data.Pclass > 1]
#只取Pclass大於2的紀錄
below_2 = data.Pclass[data.Pclass > 2]
無等距尺度實例。
符合此資料尺度的欄位為:Age/SibSp/Parch/Fare,以Fare來做示範。
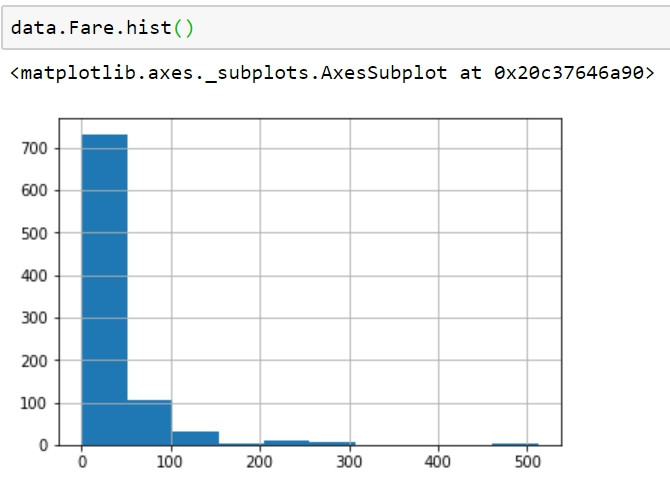
在等距尺度及更高級別如等比尺度,除了可以使用較低尺度的視覺化方式之外,它使我們還能夠使用散點圖、折線圖,以在複數軸上繪製資料(二維、三維),並將資料點可視化為圖形上的文字點,這麼做的好處是讓我們能夠比對資料間的關係(例如:線性、非線性)、變化趨勢(例如:隨時間變化的數值)。
data.Fare.hist()
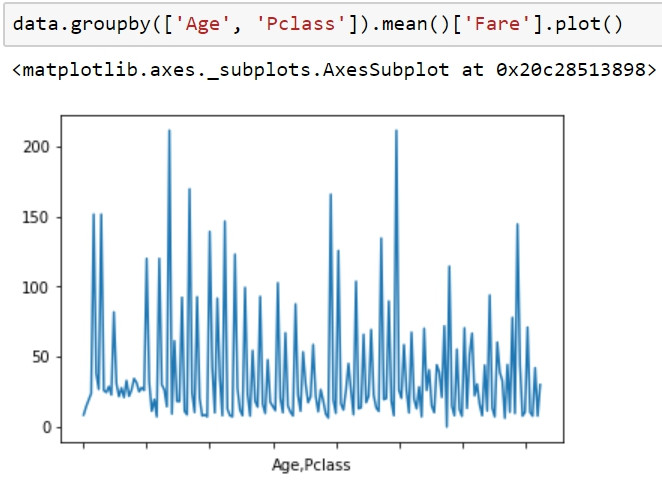
#將資料以Age以及Pclass分群後取Fare之算術平均數的折線圖
data.groupby(['Age', 'Pclass']).mean()['Fare'].plot()
#顯示所有表徵之間的關聯性
from pandas.plotting import scatter_matrix
scatter_matrix(data, alpha=0.5, diagonal='kde')
plt.show()
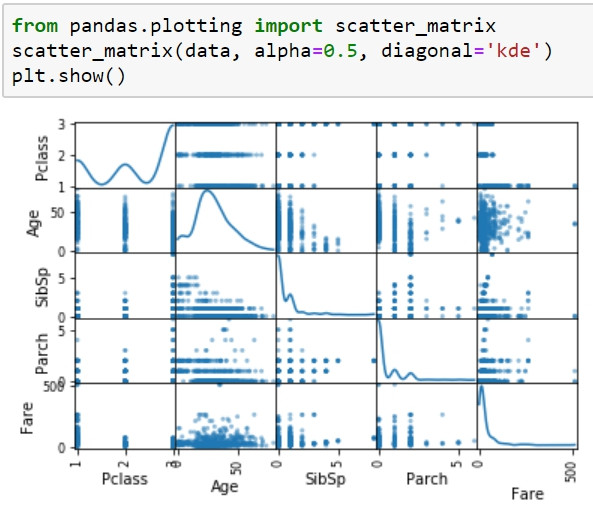
等比尺度是最高的尺度,擁有其餘尺度的特性以外,最重要的是其等比的特性允許數學中的乘除運算。例如我們想要對資料欄位Fare做其他幣別的數值轉換,完全可以將資料做乘除操作。
#將票價資料從英鎊轉換為台幣計價
fare_in_twd = data.Fare * 40.8
#將票價資料從英鎊轉換為美金計價
fare_in_twd = data.Fare * 1.31
